When to Use Fractions and When to Use Decimals on the GMAT

By QS Content Writer Updated Feb 01, 2024

Save

Introduction
Let’s look at a couple of examples where this comes in handy:
What Doesn’t Repeat?
How to Think About Our Limited Group of Fractions
This helps to answer questions such as:
Fractions for most calculations. Decimals when you’re counting places.

Need more tips for passing your GMAT? We've got you covered

Generally speaking, the GMAT would prefer that you calculate in fractions. That is, a huge proportion of the time, even when the question presents an answer in decimal form, you’ll want to convert it to fractions to calculate.

To raise your score to the 700-level, it’s absolutely vital that you learn to see no difference between, for example, $\frac{1}{4}$ and 0.25 or $\frac{1}{6}$ and 0.1666.

Being able to go back and forth between fractions and decimals comes in handy in all sorts of GMAT questions.

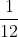Specifically, you’ll want to memorize all of the fraction-decimal equivalents from $\frac{1}{1}$ to $\frac{1}{12}$ .

Any further would just be punishing yourself--and wasting valuable brain space! Think about trying to run your laptop with only 50mb free on the hard drive. When your brain is full of useless trivia (such as the decimal equivalent of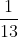 $\frac{1}{13}$ or the quadratic formula), you’ll be compromising the efficiency of that big grey processor between your ears.

Let’s look at a couple of examples where this comes in handy:

The classic GMAT question involving long division will be one where you have to determine the impact of a pattern within a repeating decimal. That might be a bit much to chew on, so let’s step back a second. All numbers that you see on the GMAT—except for ϖ and square or cube roots — will be terminating or repeating numbers.

Math People call terminating or repeating numbers “Rational Numbers.” The non-terminating, non-repeating decimals are “Irrational Numbers.”(Bear in mind that these technical terms really aren’t particularly important for GMAT purposes--and more often than not, they confuse things).

The point here is that most of the numbers you’ll encounter will be terminating or repeating decimals. In fact, all fractions either terminate or repeat.

What Doesn’t Repeat?

That’s the Irrational Numbers. These are things such as ϖ or roots of numbers that aren’t perfect squares, roots, etc.

The only Irrational Numbers you’ll see on the GMAT are ϖ and roots. Even then, you won’t need to know much more than the rough equivalents that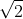 $\sqrt{2}$ = 1.4141... and 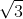$\sqrt{3}$ = 1.728...

That’s all we need to discuss, because we’re talking about fractions today. Remember, fractions means rational numbers. Always.

How to Think About Our Limited Group of Fractions

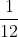Remember, we only need to look at fractions from $\frac{1}{1}$ to $\frac{1}{12}$ . Within our group, any number divided by a 3; multiple of 3 or 7; or multiple of 7 or 11 will repeat. Otherwise, it will terminate.

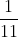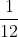
That means that, within our group, these are the fractions that repeat: $\frac{1}{3}$ , $\frac{1}{6}$ , $\frac{1}{7}$ , $\frac{1}{9}$ , $\frac{1}{11}$ , $\frac{1}{12}$

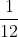Still within our $\frac{1}{1}$ to $\frac{1}{12}$ but not among this group? That means that the fraction terminates.

This helps to answer questions such as:

What is the 99^th digit after the decimal place in the decimal equivalent of 100/3?

Let’s take a look. Well,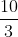 $\frac{10}{3}$ = 3.333 (because $\frac{1}{3}$ = 0.333 ). Here, notice that the decimal will definitely repeat, so its size (that is, its power of 10) is irrelevant. You can simply divide the number forgetting about the zeros and count the digits. It will ALWAYS be the same number. That is, it’s not as if the first 98 places will be 3 and the 99^th will be 7…

Let’s try another example:

What is the 99th digit after the decimal place in the decimal equivalent of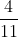 $\frac{4}{11}$ ?

The most common example that uses a repeating decimal is a situation where the decimal will repeat in a group of 3 or 4. We know that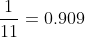 $\frac{1}{11}=0.909$

You did memorize that, right?

It follows that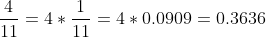 $\frac{4}{11}=4*\frac{1}{11}=4*0.0909=0.3636$ In this case, just number the decimals as they continue after 0. We see that the first digit after the zero is 3, the second is 6, the third is 3, the fourth is 6, etc. The pattern is pretty straightforward, then: odds are 3 and evens are 6. Therefore, we know that the 99^th, since it’s odd, must be 3. It’s not necessarily always evens and odds, though. Sometimes the repeating pattern is a bit different. Let’s just choose an example here—I’ve arbitrarily chosen a fraction where the terms repeat every three instead of every two: 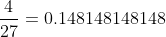$\frac{4}{27}=0.148148148148$ In the above case, look at the third, sixth, and ninth digits. Notice that they’re all 8s. In fact, every multiple of 3 will be an 8! Now, let’s assume that we want to find the 37^th digit after the 0. Just count multiples of 3. You know that every 3^rd digit will be an 8. Then all you have to do is find the closest multiple of 3: 36. Then just move one notch to the right: the 37^th is a 1. See? Not so hard.

Fractions for most calculations. Decimals when you’re counting places.

Most of the time the GMAT prefers fractions because it doesn’t allow use of calculators. Decimals will generally be used when they exhibit a particular repeating pattern. Still confused? Just learn the equivalents: once you know your fraction-decimal equivalents well, you will be able to switch back and forth with ease, picking the most useful form of the number for any given circumstance.

Related Categories:

GMAT/GRE

test prep